Jennifer Barker's Site

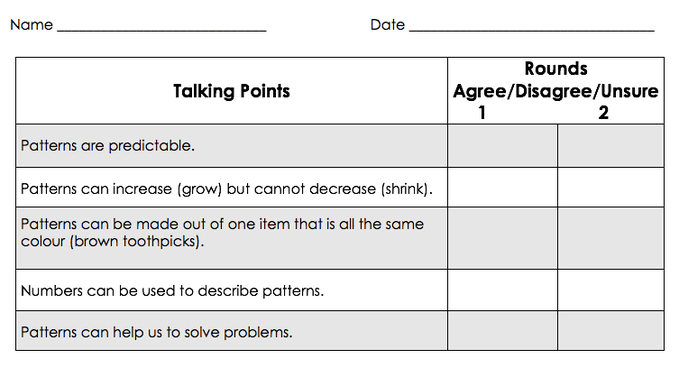
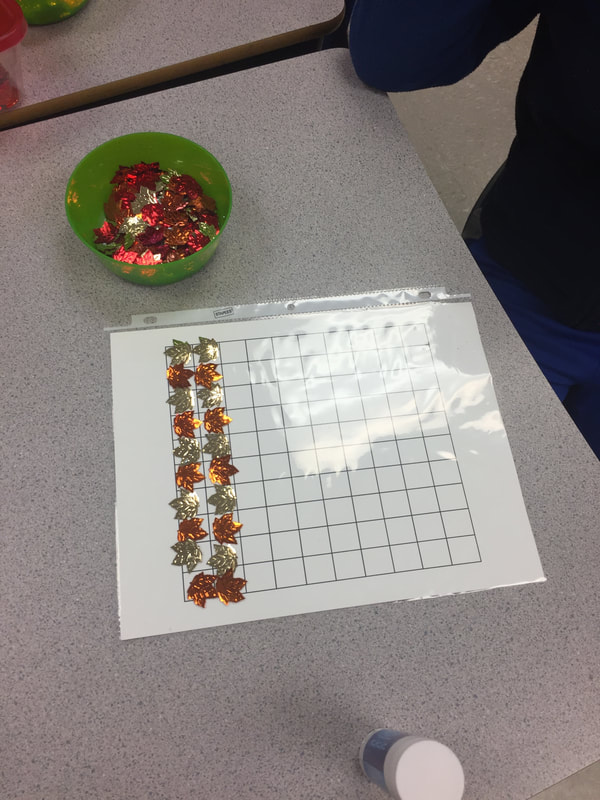
Last week I continued to work with two teachers at Betty Huff who teach Grade 3 and 3/4. On Monday, I popped by their classes to assist in introducing patterning. Inspired by Kristen's Gray's blogpost on Talking Points, which she used as a pre-assessment, we decided to try this strategy with the Grades 3/4 class to see what the students knew about patterns, as well as reveal any misconceptions they may have. We reviewed the revised curriculum for Grades 2-4, in particular the  learning standards for patterning to determine the talking points to use. I've added the word doc file for the patterning talking points below the post, should you wish to adapt these and try it with your class. 

Since "Talking Points" was new to the students, we decided to adapt it from its original version. For those of you who have never heard of Talking Points, you'll want to read either Kristen Gray's blog post or the one on Cheesemonkey Wonders site. Instead of using Talking Points in small groups, which we will do one day, it was decided to begin by using it with the whole class so the students could see how the activity works. 

Prior to coming to the carpet area, we had the students read each of the five Talking Points and where it said "Round One" they marked whether they agreed, disagreed, or were unsure of the point. Next we gathered at the carpet and each student was asked to share aloud what they wrote and give a reason why. The other students listened to each of their peers but did not add any comments. As we went around the circle in the first round, the teacher and I quickly realized that although many students agreed "Patterns are predictable," they really had very little understanding of increasing or decreasing patterns, positional patterns, using numbers to describe patterns, and whether or not patterns could help us solve problems. Most students explained that they "couldn't remember doing that last year" or "I've never tried that". This was really important formative assessment. The teacher and I realized that we needed to spend some time revisiting repeating patterns and exploring positional patterns before we could investigate increasing and decreasing patterns. We wondered whether what the children knew was representative of their knowledge or perhaps indicative of lack of experiences with these types of patterns? In speaking with another Grade 3 teacher, she mentioned that they had only worked with pattern in September and not  since. 

Being responsive to what we were hearing, we knew that moving ahead into Round Two wouldn't necessarily cause any new thinking, as so many were unsure. We decided to tweak our plans and had the students return to their tables and engage with creating patterns. We had set up materials prior to the class and in retrospect, I wish we had of provided a table area where all the materials were the same (e.g., same size and colour) such as beige toothpicks for the students to explore creating patterns using one item in creative ways such as positional patterns. There were opportunities for students to build increasing/decreasing patterns. We hoped these experiences might activate more prior knowledge and/or cause students to shift some of their thinking. 

After about 30 minutes we had the students stop what they were doing and do a gallery walk. Then we cleaned up and met back at the carpet. The students recorded their thoughts in Round Two and we went around the circle and shared again. This time, the students had more to say. Their rationales were stronger, as they could connect with an experience. We stopped after the second round because we wanted the students to have time to write in their Math Journals. We asked the students to write:

1. Which Talking Point are you sure of and why?
   
2. Which Talking Point are you unsure of and why? 

​Here are a few of their responses:

I was pleased to see how some students used examples to explain their thinking. 

The next time the teachers have the students reflect in their Math Journals, they will highlight examples like this, so students are able to see how using examples can strengthen their arguments. 

Additionally, when reading their reflections, it became evident that students did not have some of the mathematical vocabulary around patterns. For example, in the last journal below, the student wrote "...patterns are predictable because you can always know what comes next when you do 3 or 2 shapes". I wonder whether she understands the term elements or what a pattern core is? These are important for clear communication. 

I am excited to continue to use Talking Points to explore students' understanding. We will revisit these points again upon completion of this unit (and likely there will be a blogpost!). Although the teachers will wrap up the patterning unit at some point, the teachers realize that this does NOT mean they are done patterning for the year. As we know from the First Peoples Principles of Learning, "Learning takes time and patience". We need to remember that learning is recursive. Patterning WILL be revisited throughout the year. These teachers intentionally will include patterning in their daily number routines (e.g., an image of pattern is presented and students guess the rule, predict the fifth term, etc.), including patterning activities daily math investigations and weekly rich problems, and whenever it makes sense to do so. 

​Today I had the pleasure of working with a lovely Kindergarten class at Jessie Lee Elementary to introduce Counting Collections.

I began by reading aloud the book If A Chicken Stayed for Supper by Carrie Weston. In this delightful tale, five little foxes sneak out of their den, despite being told by their mother to stay home while she goes out looking for dinner. While out playing, the foxes begin to worry that perhaps one of them may get lost in the dark. The eldest fox, Tufty, decides she will take charge and count her brothers and sisters. She taps each fox on their nose but forgets to count herself and mistakenly thinks they have lost someone. All of the foxes begin to cry. Next, the second eldest fox, Mufty, tries his best to count, pulling each fox's tail but again he forgets to count himself and ends up with a count of four. Again, the foxes think they are one short. In the end Mother Hen comes to the rescue and lines up all the foxes and taps each one on their head. The foxes yap with joy! "You've found one of us! Thank you! Thank You!" 

I use this engaging story to springboard children's ideas about strategies they can use to keep track of quantities when counting. We discuss, what different ways did the foxes and Mother Hen use to help keep track? How do you keep track? To assist the students with one-to-one correspondence, we provided five and ten frames, as well as small soup cups for the students to use should they wish to. We explored how these 'tools' help us to organize our items and potentially see groups of items. For many students, having cups available to place one counting collection item in at a time, helped them to keep track. Sometimes at this age children will skip an item when counting or count the same item twice.  Additionally, not all children have a solid understanding of the stable order of the numbers (e.g., they might say "one, two, three, five"... skipping four). Counting collections provides a wonderful opportunity for one-to-one correspondence, learning the correct of numbers, and cardinality (knowing the last number you say represents the total amount of the set) .

For more information about Counting Collections, please check this blogpost and under the Ideas section - Counting Collections. 

Sept 29th update:
An important point another Numeracy Teacher (thank you Janice) reminded me of, is the focus on working with partners in September. Counting Collections is something we do with others. In the K class on Wednesday we discussed how we work with partners. How do we respond to a partner when we hear there name called with ours? We modelled some positive options, including giving a "high five" and saying "I'm happy to be your partner". In a respectful classroom community, students need to understand that they will be required to work with others in friendly ways. We included the students in helping us to determine how to work out who chooses the counting collection bag and who chooses the tools. On this day, it was determined that the taller partner would choose the collections. We also modelled how to help each other to organize the collections and take turns counting. 

I've also had some questions about the yellow stickies. I've always had stickies and markers  available in my tool kits for students who wish to record their estimate and/or to record their actual count. At this point in the year in Kindergarten, many students are just learning how to form numerals, so writing the numerals should NOT be a requirement. The stickies are there if students wish to use them, but many won't and this is fine. In reflection, I think I would take the stickies and markers out of my tools bin when working with Kindergarten students for the first several months, as writing numerals is not one of the learning intentions of this activity. If teachers were wondering whether their students could match a quantity to a numeral, there are many other, more engaging ways to do this (e.g., build a set, roll and make the matching playdough number)

This week I visited a Grades 3 and Grades 3/4 class at Betty Huff Elementary. The two teachers and I met during the first week of school and worked collaboratively to discuss how to begin the year. I am working with these teachers this term to support their professional inquires which focus on developing their students curricular competencies in relation to content, as well exploring what inquiry-based practices could look like in mathematics.

​We began by creating a mini-unit exploring the following questions: What is math? What does it mean to do math? Where does math live in the world? Additionally, we wanted students to begin to explore their own identity as a math learner. This is an important aspect of BC's redesigned curriculum. The Positive Personal and Cultural Identity is one of our core competencies and includes the awareness, understanding, and appreciation of all the facets that contribute to a healthy sense of oneself . We wondered how our students saw themselves as Mathematicians. 

​We began with an activity I had seen on Graeme Anshaw's blog where he asked students to share their personal histories with mathematics. The teachers gave each student a sticky and ask them to write or draw how they felt about math and why. Then students were invited to share their thoughts with the class and place their sticky on the line spectrum. The teachers commented how through this activity they were able to learn about the mindsets students held with regard to mathematics. As you can see the Grade 3/4 class held more positive views, while the Grade 3 class was more mixed. The teachers remarked how curious they were to dig more deeply into these stories and work with these students to shift some of their negative feelings. 

I visited the class on the second day of the mini-unit. We began with the question "What is Mathematics?", and surprisingly, we learned that not all children had an understanding of the word "Mathematics". They didn't realize it was just a longer version of the word "Math"... an important reminder that all children are "mathematics language learners" and we must pay attention to the language we use. 

When reflecting upon the charts, we were able to see similarities to the work that Tracy Zager and Deborah Nichols reported hearing from a Grades 1/2 class (pg. 11 - 13 in Becoming The Math Teacher You Wish You'd Had). It seemed that our students felt mathematics was mostly about computation. Their experiences had been many worksheets, which they felt was really hard. 

Inspired by Tracy Zager's suggestions to use books to help expand children's view of mathematics, we read aloud On A Beam of Light: A Story of Albert Einstein by Jennifer Berne. Before beginning the book, we passed out "Notice/Wonder" sticks to the students. We asked them to raise their "Notice" glasses if they noticed anything in the book that they thought represented mathematics, which we would add to the chart. Additionally, student were asked to raise their "Wonder" question marks if they thought they might have seen or heard something that could be added to our chart, but were unsure. Credits go out to Beth Kobett who shared the idea of Notice and Wonder sticks on Twitter. 

Below is the mini-unit we created including using ideas from Tracy Zager's book, Jo Boaler's inspirational week of maths, and Graeme Anshaw's blog. Feel free to leave any feedback you have on our mini-unit. We welcome your ideas and suggestions! I am curious how did you start your year with your Mathematicians?